matematica vs trigoOnometria

miércoles, 6 de abril de 2011

SIMÓN RODRÍGUEZ

Nace en Caracas Simón Rodríguez, calificado de "loco", "maestro" o "don", este ejemplar venezolano, de padres desconocidos, el 28 de octubre de 1771. Se dice que fue hijo adoptivo de Cayetano Carreño y de Rosalía Rodríguez. De su infancia, se conoce muy poco. Simón Rodríguez es un niño expósito y su único familiar conocido es su hermano Gayetano.
Su carácter nada común lo lleva a quitarse el apellido paterno, el adoptivo y a quedarse sólo con el de su madre (originalmente se hubiera llamado Simón Carreño Rodríguez), por eso es que, el mismo Simón se presenta como expósito en el acta matrimonial.

Se caracterizará toda su vida por seguir apasionadamente su ideal de pensar y enseñar en libertad plena. Su vida estuvo dominada por la pasión de las letras.
El primer contacto de los dos Simones se produce cuando Rodríguez es contratado por Feliciano Palacios, abuelo de Bolívar, para que en su propia casa le sirva de amanuense. Más tarde, al fugarse de la casa de su tío Carlos Palacios, Bolívar ingresará a la escuela pública de Rodríguez.

Este era un maestro que enseñaba divirtiendo, según expresión bolivariana. Su manera de enseñar, distinta a todo lo tradicional, era en el campo, frente a la naturaleza, lo cual servía para el espíritu, para la fortaleza del cuerpo y para el conocimiento de las cosas que nos rodean. Si está en el aula, entre sus 114 alumnos (setenta y cuatro que pagan y cuarenta gratis, entre ellos nueve expósitos), les da instrucción adecuada a sus edades y les inculca las buenas costumbres y el amor por la libertad.

Don Simón Rodríguez, precursor y animador de la inquietud bolivariana, es por antonomasia el Maestro del Libertador; antes de que éste independizara a América, Rodríguez (su "Maestro Universal") hace su tarea: independiza a Bolívar, lo divorcia de la realidad tradicional y lo acerca a la verdad futura; le ayuda a conseguir la perspectiva propia de un creador, a intuir su faena y a calcular las fuerzas de sus auxiliares y sus enemigos. Simón Rodríguez llama a Bolívar a ser terriblemente cuerdo entre aquellos mediocres que se autoestiman depositarios del buen juicio y de la sensatez, y a los ojos de los cuales la Independencia tenía que ser una locura singular.
La enseñanza de Rodríguez se cumple en la adolescencia y en los umbrales mismos de su edad adulta; superados algunos rices de la infancia entre maestro y discípulo, roces que nunca más recordará El Libertador, la compenetración entre ambos es intensa y duradera. Por el carácter independiente y rebelde de Rodríguez se comprende que cale tan hondo en el espíritu del joven.

La casualidad pone en manos de Simón Rodríguez, pedagogo per sé y fanático de Juan Jacobo Rousseau, a un niño sano, rico, de alcurnia, inteligente, sin familia, sin padres siquiera a quienes rendir estrecha cuenta de aquella infancia. En suma, encuentra el Emilio ideal. Y Simón Rodríguez inicia la educación que aconseja Rousseau en su Emilio. Bolívar es el primer hombre moderno, quizás el único, que haya sido educado para hombre libre. Rodríguez le hizo cerrar los libros de texto y le abrió el gran libro de la naturaleza. Le enseña antes que nada a ser fuerte de alma y de cuerpo; y a convivir con la naturaleza, sin ser víctima de ella. Le enseña a dar grandes caminatas, a cabalgar días enteros, a nadar, a saltar. Le transmite oralmente cuanto el discípulo puede asimilar. Y le obliga a leer a los grandes autores clásicos como Plutarco y a los modernos como Rousseau. A eso se limita.

Simón Rodríguez, en 1794 presentó al Cabildo de Venezuela un proyecto de Escuelas Públicas, donde analizaba el sistema educativo para aquel entonces y donde planteaba la necesidad de la participación activa de los alumnos en las cátedras, exponiendo sus ideas y aclarando sus dudas. Pero las autoridades coloniales no le prestaron ninguna atención.

Simón Rodríguez, además, de su conocimiento y talento como educador, sintió también la inquietud de la Libertad; participó en el movimiento revolucionario de Gual y España, y complicado en esta tentativa de independencia abandonó el país al fracasar el movimiento y se traslada a Jamaica, suplantando su nombre por el de Samuel Robinson, para evitar cualquier vengativa por parte de las autoridades del rey.

Al llegar a Jamaica en 1798, se inscribió en una escuela pública para aprender ingles, donde hizo buenas relaciones con los niños, que eran sus compañeros de clase, debido a su bondadoso corazón. Luego marchó a los Estados Unidos, estableciéndose en Baltimore, donde se desempeñó por algún tiempo como cajista de una imprenta. Simón Rodríguez tenía un espíritu de aventurero y esto lo llevo a seguir recorriendo varios países. Simón Rodríguez solía decir: "No quiero parecerme a los árboles, que echan raíces en un solo lugar; sino al viento, al agua, al sol, a todas esas cosas que marchan sin cesar".
Viajó por espacio de diez y seis años, conoció Italia, Suiza, Alemania, Bélgica, Rusia, Inglaterra y otros. Su estadía en el viejo continente le permite dominar el francés, el italiano, el alemán y el portugués, profundizar sus estudios filosóficos y entrar en contacto con las teorías revolucionarias que pronto implantarían un nuevo orden político y social de alcance mundial. Todos estos conocimientos, más tarde los vertería en su más destacado alumno: el LibertadorSimón Bolívar.
Simón Bolívar viaja a Europa para distracción de su viudez temprana, dura tres años por fuera, donde se encuentra con su Maestro Simón Rodríguez y se convierte en un viaje de aprendizaje, ya que Rodríguez vuelca todos sus conocimientos en él. En esta época Rodríguez le aconseja a Bolívar que estudie a "Helvecio, Holbach, Hume", entre otros.
En 1823, vuelve Simón Rodríguez a Venezuela, cuando su antiguo discípulo Simón Bolívar se encontraba preparando la emancipación del Perú. Al enterarse Bolívar de la llegada de su maestro lo llama a su lado y lo nombra Director e Inspector de Instrucciones Públicas y Beneficencia, y regenta la Escuela Municipal de Caracas. Y en calidad de tal acompaña al Libertador a Chuquisaca, donde funda una escuela, acorde con sus ideas de enseñanza. Se esmera en hacer de sus alumnos albañiles, herreros, carpinteros y otros oficios manuales. Pero lamentablemente fracasa, porque los mismos padres de familia miraban con desagrado que sus hijos aprendieran tales oficios, teniendo que cerrar la escuela.

Bolívar ratificó en 1823 la manera de enseñanza de Rodríguez sobre las buenas costumbres y el amor a la libertad: «Usted formó mi corazón para la libertad, para la justicia, para lo grande, para lo hermoso».
En 1826 Rodríguez le escribía a Bolívar: "No sé si usted se acuerda que estando en París, siempre tenía yo la culpa de cuanto sucedía a Toro, Montúfar, a usted y a todos sus amigos". Palabras que sugieren la gran amistad entre aquellos jóvenes y el travieso pero respetado Pedagogo. Esto haciendo remembranza de la época que pasaron juntos en París cuando bolívar viajó a Europa.
En ese entonces, Rodríguez solo contaba con treinta años.
En 1829, retirado de la docencia, establece en Azángaro, sobre las riberas del Lago de Titicacas, una fábrica de Velas, que irónicamente él llamaba "De luces americanas". Pero reclamado por la población cedió a encargarse de nuevo de la Educación.
Después de la muerte del Libertador, en 1830, se traslada a Lima y luego a Huacho. En 1833, fue nombrado Director de estudios del Departamento de Concepción, este mismo año, en Chile se entrevista con su compatriota Andrés Bello y funda una escuela de Barrio. Después de algunos años de permanencia en aquella República, pasó a la del Ecuador donde fue nombrado catedrático de Botánica y Agricultura del Colegio de Latacunga.
En 1846, regenta un Colegio en Quito y en 1847, se traslada al Sur de Colombia, entregado siempre a su pasión de enseñar. Luego se enrumba a Perú, donde murió Simón Rodríguez, pobre y sin hogar a los 83 años de edad, el 23 de Febrero de 1854, en el humilde pueblecito peruano San Nicolás de Amotape. Fabricaba velas, que es hacer luz.

Sus restos fueron trasladados en 1954 al Panteón Nacional, en el centenario de su muerte.
No sin motivos, Bolívar usaba el calificativo de «el Sócrates de Colombia» para referirse a su maestro.
Simón Rodríguez, fue un maestro ejemplar y gran luchador por la Libertad y la Justicia.
Escribió obras de valioso interés, entre las que se pueden citar:
Educación Popular.
El suelo y sus habitantes.
Tratado sobre las luces y las virtudes sociales.
Defensa de Bolívar.
El Libertador del Mediodía de América.
Sus compañeros de armas defendidos por un amigo de la causa social..................................

martes, 15 de febrero de 2011

trigonometria inversa

Las funciones trigonométricas

Artículo principal: Función trigonométrica

La trigonometría como rama de las matemáticas realiza su estudio en la relación entre los lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría y sus aplicaciones. Para el desarrollo de este fin se definieron una serie de funciones que han sobrepasado su fin original, convirtiéndose en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.

[editar] Razones trigonométricas

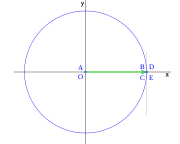
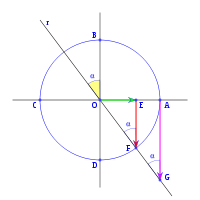
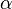El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo $\alpha \,$ , correspondiente al vértice A, situado en el centro de la circunferencia.

El seno (abreviado como sen, o sin por llamarse "senos" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,

$\operatorname {sen} \, \alpha = \frac{\overline{CB}}{\overline{AB}} = \frac{a}{c}$

El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

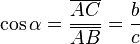
$\cos\alpha = \frac{\overline{AC}}{\overline{AB}} = \frac{b}{c}$

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

$\tan\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{a}{b}$

[editar] Razones trigonométricas recíprocas

La Cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:

$\csc \alpha = \frac{1}{\operatorname {sen} \; \alpha} = \frac{c}{a}$

En el esquema su representación geométrica es:

$\csc \alpha = \overline{AG}$

La Secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:

$\sec \alpha = \frac{1}{\operatorname {cos} \; \alpha} = \frac{c}{b}$

En el esquema su representación geométrica es:

$\sec \alpha = \overline{AD}$

La Cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:

$\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}$

En el esquema su representación geométrica es:

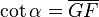
$\cot \alpha = \overline{GF}$

Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés específico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse.

[editar] Otras funciones trigonométricas

Además de las funciones anteriores existen otras funciones trigonométricas, matemáticamente se pueden definir empleando las ya vistas, su uso no es muy corriente, pero si se emplean dado su sentido geométrico, veamos:
El seno cardinal o función sinc (x) definida:

$\operatorname {sinc} \; (x) = \frac{\sin(x)}{x}$

El verseno, es la distancia que hay entre la cuerda y el arco en una circunferencia, también se denomina sagita o flecha, se define:

$\operatorname {versen} \; \alpha = 1 - \cos \alpha$

El semiverseno, se utiliza en navegación al intervenir en el cálculo esférico:

$\operatorname {semiversen} \; \alpha = \frac {\operatorname {versen} \; \alpha }{2}$

El coverseno,

$\operatorname {coversen} \; \alpha = 1 - \operatorname {sen} \; \alpha$

El semicoverseno

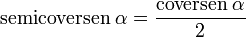
$\operatorname {semicoversen} \; \alpha = \frac { \operatorname {coversen} \; \alpha }{2}$

El exsecante:

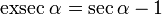
$\operatorname {exsec} \; \alpha = \sec \alpha - 1$

[editar] Funciones trigonométricas inversas

En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco,

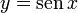
$y= \operatorname {sen} \, x \,$

y es igual al seno de x, la función inversa:

$x = \operatorname {arcsen} \; y \,$

x es el arco cuyo seno vale y, o también x es el arcoseno de y.
si:

$y= \cos x \,$

y es igual al coseno de x, la función inversa:

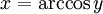
$x = \arccos y \,$

x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.
si:

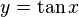
$y= \tan x \,$

y es igual al tangente de x, la función inversa:

$x = \arctan y \,$

x es el arco cuya tangente vale y, o x es igual al arcotangente de y.

Sentido de las funciones trigonométricas

Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circunferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.
Nótese que el punto A es el vértice del triángulo, y O es el centro de coordenada del sistema de referencia:

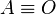
$A \equiv O$

a todos los efectos.
La recta r, que pasa por O y forma un ángulo $\alpha \,$ sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
Por semejanza de triángulos:

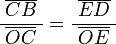
$\frac{\; \overline{CB} \;}{\overline{OC}} = \frac{\; \overline{ED} \;}{\overline{OE}}$

Los puntos E y B están en la circunferencia de centro O, por eso la distancia $\overline{OE}$ y $\overline{OB}$ son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:

$\operatorname {sen} \alpha = \overline{CB} \,$

$\cos \alpha = \overline{OC} \,$

$\tan \alpha = \overline{ED} \,$

tenemos:

$\frac{\operatorname {sen} \alpha}{ \cos \alpha} = \frac{\tan \alpha}{1}$

La tangente es la relación del seno entre el coseno, según la definición ya expuesta.

[editar] Primer cuadrante

Para ver la evolución de las funciones trigonométricas según aumenta el ángulo, daremos una vuelta completa a la circunferencia, viéndolo por cuadrantes, los segmentos correspondientes a cada función trigonométrica variaran de longitud, siendo esta variación función del ángulo, partiendo en el primer cuadrante de un ángulo cero.
Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo $\alpha \,$ .
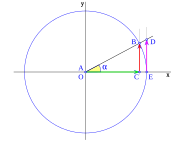
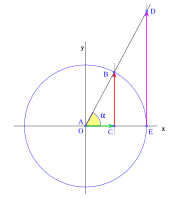
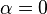Para $\alpha = 0 \,$ , tenemos que B, D, y C coinciden en E, por tanto: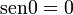

$\operatorname {sen} 0 = 0 \,$

$\cos 0 = 1 \,$

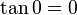
$\tan 0 = 0 \,$

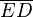Si aumentamos progresivamente el valor de $\alpha \,$ , las distancias $\overline{CB}$ y $\overline{ED}$ aumentarán progresivamente, mientras que $\overline{OC}$ disminuirá.
Percatarse que el punto B es de la circunferencia y cuando el ángulo aumenta se desplaza sobre ella.
El punto E es la intersección de la circunferencia con el eje x y no varia de posición.
Los segmentos: $\overline{OC}$ y $\overline{CB}$ están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero $\overline{ED}$ no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo $\alpha = 0,5 \pi \,$ rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia $\overline{ED}$ será infinita.
El punto C coincide con A y el coseno vale cero. El punto B esta en el eje y en el punto más alto de la circunferencia y el seno toma su mayor valor: uno.
Para un ángulo recto las funciones toman los valores:

$\operatorname {sen} \frac{\pi}{2} = 1 \,$

$\cos \frac{\pi}{2} = 0 \,$

$\tan \frac{\pi}{2} = \infty \,$

Cálculo de algunos casos

Partiendo de una circunferencia de radio uno, dividida en cuatro cuadrantes, por dos rectas perpendiculares, que se cortan en el centro de la circunferencia O, estas rectas cortan a la circunferencia en los puntos A, B, C y D, la recta horizonte AC también la podemos llamar eje x y la recta vertical BD eje y. Dada una recta r, que pasa por el centro de la circunferencia y forma un ángulo α con OA, eje x, y corta a la circunferencia en F, tenemos que la vertical que pasa por F corta al eje x en E, la vertical que pasa por A corta a la recta r en G. Con todo esto definimos, como ya se vio anteriormente, las funciones trigonométricas:
para el seno:

$sen \; \alpha = \cfrac{\; \overline{EF} \;}{\overline{OF}} = \overline{EF}$

dado que:

$\overline{OF} = 1$

Para el coseno:

$cos \; \alpha = \cfrac{\; \overline{OE} \;}{\overline{OF}} = \overline{OE}$

dado que:

$\overline{OF} = 1$

Para la tangente:

$tan \; \alpha = \cfrac{\; \overline{EF} \;}{\overline{OE}} = \cfrac{\; \overline{AG} \;}{\overline{OA}} = \overline{AG}$

dado que:

$\overline{OA} = 1$

partiendo de estas definiciones, podemos ver algunos caso importantes:

[editar] Para 90-α

Si a partir del eje vertical OB trazamos la recta r a un ángulo α en el sentido horario, la recta r forma con el eje x un ángulo 90-α, el valor de las funciones trigonométricas de este ángulo conocidas las de α serán:
El triángulo OEF rectángulo en E, siendo el ángulo en F α, por lo tanto:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = sen \; (90-\alpha) \end{array} \right \} \longrightarrow \quad sen \; (90-\alpha) = cos \; \alpha$

en el mismo triángulo OEF, tenemos que:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = cos \; (90-\alpha) \end{array} \right \} \longrightarrow \quad cos \; (90-\alpha) = sen \; \alpha$

viendo el triángulo OAG, rectángulo en A, siendo el ángulo en G igual a α, podemos ver:

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =1 \\ \overline{AG} = tan \; (90-\alpha) \end{array} \right \} \longrightarrow \quad tan \; (90-\alpha) = \cfrac{1}{tan \; \alpha}$

[editar] Para 90+α

Si a partir de eje vertical OB trazamos la recta r a un ángulo α, medido en sentido trigonométrico, el ángulo formado por el eje horizontal OA y la recta r será 90+α. La prolongación de la recta r corta a la circunferencia en F y a la vertical que pasa por A en G.
El triángulo OEF es rectángulo en E y su ángulo en F es α, por lo tanto tenemos que:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = sen \; (90+\alpha) \end{array} \right \} \longrightarrow \quad sen \; (90+\alpha) = cos \; \alpha$

En el mismo triángulo OEF podemos ver:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = -cos \; (90+\alpha) \end{array} \right \} \longrightarrow \quad cos \; (90+\alpha) = -sen \; \alpha$

En el triángulos OAG rectángulo A y siendo α el ángulo en G, tenemos:

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =1 \\ \overline{AG} = -tan \; (90+\alpha) \end{array} \right \} \longrightarrow \quad tan \; (90+\alpha) = \cfrac{-1}{tan \; \alpha}$

[editar] Para 180-α

Si sobre el eje horizontal OC, trazamos la recta r a un ángulo α, el ángulo entre el eje OA y la recta r es de 180-α, dado el triángulo OEF rectángulo en E y cuyo ángulo en O es α, tenemos:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = sen \; (180-\alpha) \end{array} \right \} \longrightarrow \quad sen \; (180-\alpha) = sen \; \alpha$

en el mismo triángulo OEF:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = -cos \; (180-\alpha) \end{array} \right \} \longrightarrow \quad cos \; (180-\alpha) = -cos \; \alpha$

En el triángulo OAG, rectángulo en A y con ángulo en O igual a α, tenemos:

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{AG} \;}{\overline{OA}} \\ \overline{OA} =1 \\ \overline{AG} = -tan \; (180-\alpha) \end{array} \right \} \longrightarrow \quad tan \; (180-\alpha) = -tan \; \alpha$

[editar] Para 180+α

Sobre la circunferencia de radio uno, a partir del eje OC con un ángulo α trazados la recta r, el ángulo del eje OA y la recta r es de 180+α, como se ve en la figura. En el triángulo OEF rectángulo en E se puede deducir:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = -sen \; (180+\alpha) \end{array} \right \} \longrightarrow \quad sen \; (180+\alpha) = -sen \; \alpha$

en el mismo triángulo OEF tenemos:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = -cos \; (180+\alpha) \end{array} \right \} \longrightarrow \quad cos \; (180+\alpha) = -cos \; \alpha$

en el triángulo OAG, rectángulo en A, vemos que:

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{AG} \;}{\overline{OA}} \\ \overline{OA} =1 \\ \overline{AG} = tan \; (180+\alpha) \end{array} \right \} \longrightarrow \quad tan \; (180+\alpha) = tan \; \alpha$

[editar] Para 270-α

Sobre el eje OD y con un ángulo α medido en sentido horario trazamos la recta r. El ángulo entre el eje OA y la recta r es de 270-α. En el triángulo OEF, rectángulo en E, tenemos:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = -sen \; (270-\alpha) \end{array} \right \} \longrightarrow \quad sen \; (270-\alpha) = -cos \; \alpha$

por otra parte en el mismo triángulo OEF, tenemos:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = -cos \; (270-\alpha) \end{array} \right \} \longrightarrow \quad cos \; (270-\alpha) = -sen \; \alpha$

en el triángulo OAG rectángulo en A, y siendo α el ángulo en G, tenemos;

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =1 \\ \overline{AG} = tan \; (270-\alpha) \end{array} \right \} \longrightarrow \quad tan \; (270-\alpha) = \cfrac{1}{tan \; \alpha}$

[editar] Para 270+α

Sobre el eje OD y con un ángulo α medido en sentido trigonométrico, trazamos la recta r. El ángulo entre el eje OA y la recta r es de 270+α. En el triángulo OEF, rectángulo en E, tenemos:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = -sen \; (270+\alpha) \end{array} \right \} \longrightarrow \quad sen \; (270+\alpha) = -cos \; \alpha$

por otra parte en el mismo triángulo OEF, tenemos:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = cos \; (270+\alpha) \end{array} \right \} \longrightarrow \quad cos \; (270+\alpha) = sen \; \alpha$

en el triángulo OAG rectángulo en A, y siendo α el ángulo en G, tenemos;

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =1 \\ \overline{AG} = -tan \; (270+\alpha) \end{array} \right \} \longrightarrow \quad tan \; (270+\alpha) = \cfrac{-1}{tan \; \alpha}$

[editar] Para -α

Sobre la circunferencia de radio uno, a partir del eje OA con un ángulo α medido en sentido horario trazados la recta r, el ángulo del eje OA y la recta r es de -α, o lo que es lo mismo 360-α como se ve en la figura. En el triángulo OEF rectángulo en E se puede deducir:

$\left . \begin{array}{l} sen \; \alpha =\cfrac{\; \overline{EF} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{EF} = -sen \; (-\alpha) \end{array} \right \} \longrightarrow \quad sen \; (-\alpha) = -sen \; \alpha$

en el mismo triángulo OEF tenemos:

$\left . \begin{array}{l} cos \; \alpha =\cfrac{\; \overline{OE} \;}{\overline{OF}} \\ \overline{OF} =1 \\ \overline{OE} = cos \; (-\alpha) \end{array} \right \} \longrightarrow \quad cos \; (-\alpha) = cos \; \alpha$

en el triángulo OAG, rectángulo en A, vemos que:

$\left . \begin{array}{l} tan \; \alpha =\cfrac{\; \overline{AG} \;}{\overline{OA}} \\ \overline{OA} =1 \\ \overline{AG} = -tan \; (-\alpha) \end{array} \right \} \longrightarrow \quad tan \; (-\alpha) = -tan \; \alpha$

[editar] Identidades trigonométricas

Artículo principal: Identidades trigonométricas

Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable. En trigonometría existen seis identidades fundamentales:

[editar] Recíprocas

$\operatorname {sen} (\alpha) \cdot \csc (\alpha) = 1$

$\operatorname {cos} (\alpha) \cdot \sec (\alpha) = 1$

$\operatorname {tan} (\alpha) \cdot \cot (\alpha) = 1$

[editar] De división

$\tan (\alpha) = \frac {\operatorname {sen} (\alpha)}{ \cos (\alpha)}$

[editar] Por el teorema de Pitágoras

Como en el triángulo rectángulo cumple la función que:

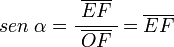
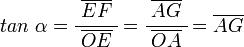
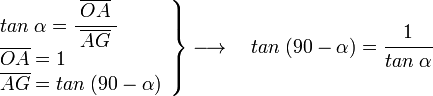
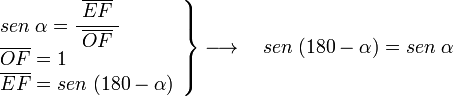
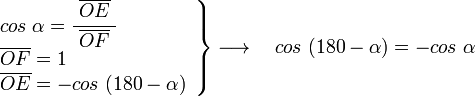
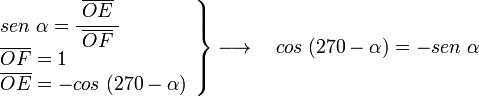
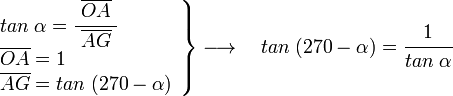
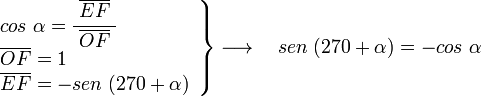
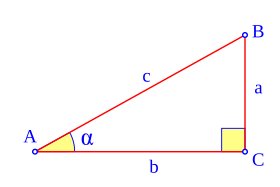
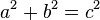
$a^2 + b^2 = c^2 \,$

de la figura anterior se tiene que:

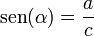
$\operatorname {sen} (\alpha ) = \frac {a}{c}$

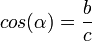
$cos (\alpha ) = \frac {b}{c}$

por tanto:

$\operatorname {sen}^2 \alpha + \cos^2 \alpha = \bigg(\dfrac {a}{c}\bigg) ^2 + \bigg(\frac {b}{c}\bigg)^2 = \frac {a^2 + b^2 }{c^2} = \frac {c^2}{c^2} = 1$

entonces para todo ángulo α, se cumple la identidad Pitagórica:

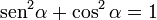
$\operatorname {sen}^2 \alpha + \cos^2 \alpha = 1 \,$

que también puede expresarse:

$\tan^2 \alpha + 1 = \sec^2 \alpha \,$

$1+\cot^2 \alpha = \csc^2 \alpha \,$

[editar] Suma y diferencia de dos ángulos

$\operatorname {sen}(\alpha + \beta) = \operatorname {sen} \alpha \cos \beta + \cos \alpha \operatorname {sen} \beta \,$

$\operatorname {sen}(\alpha - \beta) = \operatorname {sen} \alpha \cos \beta - \cos \alpha \operatorname {sen} \beta \,$

$\cos(\alpha + \beta) = \cos \alpha \cos \beta - \operatorname {sen} \alpha \operatorname {sen} \beta \,$

$\cos(\alpha - \beta) = \cos \alpha \cos \beta + \operatorname {sen} \alpha \operatorname {sen} \beta \,$

$\begin{align} & {\mathrm{\vdash}\cos{\mathrm{(}}{x}\mathrm{{-}}{y}{\mathrm{)}}\mathrm{{=}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {{i}{\mathrm{)}}{Se}\;{parte}\;{de}{\mathrm{:}}}\\ & {}\\ & {\sin{\mathrm{(}}{x}\mathrm{{-}}{y}{\mathrm{)}}\mathrm{{=}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{-}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {{ii}{\mathrm{)}}{Se}\;{deriva}\;{la}\;{igualdad}{\mathrm{,}}\;{entonces}{\mathrm{:}}}\\ & {}\\ & {\frac{d}{dx}\sin{\mathrm{(}}{x}\mathrm{{-}}{y}{\mathrm{)}}\mathrm{{=}}\frac{d}{dx}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{-}}\frac{d}{dx}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{-}}{\mathrm{(}}\mathrm{{-}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{))}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {\mathrm{\therefore}\;{queda}\;{demostrada}\;{la}\;{igualdad}{\mathrm{.}}}\\ & {} \end{align}$

$\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}$

$\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta}$

[editar] Suma y diferencia del seno y coseno de dos ángulos

$\operatorname {sen} \alpha + \operatorname {sen} \beta = 2\operatorname {sen} \left( \frac{\alpha + \beta}{2}\right)\cos \left(\frac{\alpha - \beta}{2} \right)$

$\operatorname {sen} \alpha - \operatorname {sen} \beta = 2\operatorname {sen} \left( \frac{\alpha - \beta}{2}\right)\cos \left(\frac{\alpha + \beta}{2} \right)$

$\cos \alpha + \cos \beta = 2\cos \left(\frac{\alpha + \beta}{2} \right)\cos \left(\frac{\alpha - \beta}{2}\right)$

$\cos \alpha - \cos \beta = -2\operatorname {sen} \left(\frac{\alpha + \beta}{2} \right) \operatorname {sen} \left(\frac{\alpha - \beta}{2}\right)$

[editar] Producto del seno y coseno de dos ángulos

$\cos(\alpha) \cos(\beta) = \frac{\cos(\alpha + \beta) + \cos(\alpha - \beta) }{ 2}$

$\operatorname {sen}(\alpha) \operatorname {sen}(\beta) = \frac{\cos(\alpha - \beta) - \cos(\alpha + \beta) }{ 2}$

$\operatorname {sen}(\alpha) \cos(\beta) = \frac{\operatorname {sen}(\alpha + \beta) + \operatorname {sen}(\alpha - \beta) }{ 2}$

$\cos(\alpha) \operatorname {sen}(\beta) = \frac{\operatorname {sen}(\alpha + \beta) - \operatorname {sen}(\alpha - \beta) }{ 2}$

[editar] Ángulo doble

$\operatorname {sen} 2\alpha = 2 \operatorname {sen}\alpha \cdot \cos \alpha \,\!$

$\cos 2\alpha = \cos^2 \alpha - \operatorname {sen}^2 \alpha \,\!$

$\cos 2\alpha = 1 - 2 \operatorname {sen}^2 \alpha \,\!$

$\cos 2\alpha = -1 + 2 \cos^2 \alpha \,\!$

$\tan 2\alpha = \frac{2\tan \alpha}{1 - \tan^2 \alpha}$

$\operatorname {sen}^2 \alpha = \frac{1-\cos 2\alpha}{2}$

$\cos^2 \alpha = \frac{1+\cos 2\alpha}{2}$

[editar] Ángulo mitad

$\operatorname {sen}\left(\frac{\alpha}{2} \right) = \sqrt{\frac{1-\cos\alpha}{2}} \,\!$

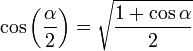
$\cos \left(\frac{\alpha}{2} \right) = \sqrt{\frac{1+\cos\alpha}{2}} \,\!$

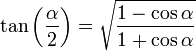
$\tan \left(\frac{\alpha}{2} \right) = \sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}}$

$\begin{align} & {\mathrm{\vdash}\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{\sin\mathrm{(}u\mathrm{)}}}\\ & {}\\ & {{i}{\mathrm{)}}\;{Se}\;{parte}\;{de}\;\tan{\mathrm{(}}{x}{\mathrm{)}}\mathrm{{=}}\frac{\sin\mathrm{(}x\mathrm{)}}{\cos\mathrm{(}x\mathrm{)}}{\mathrm{,}}\;{entonces}{\mathrm{:}}}\\ & {}\\ & {\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\frac{\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{2}}}{\sqrt{\frac{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{2}}}}\\ & {}\\ & {{ii}{\mathrm{)}}\;{Se}\;{multiplica}\;{por}\;{uno}\;{para}\;{\mathrm{eliminar}}\;{las}\;{raices}\;{de}\;{dos}{\mathrm{:}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\frac{\sqrt{2}}{\sqrt{2}}\mathrm{\cdot}\frac{\mathrm{(}\tfrac{\sqrt{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}{\sqrt{2}}\mathrm{)}}{\mathrm{(}\tfrac{\sqrt{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}{\sqrt{2}}\mathrm{)}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\frac{\sqrt{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}{\sqrt{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {{iii}{\mathrm{)}}\;{Se}\;{multiplica}\;{otra}\;{vez}\;{por}\;{un}\;{uno}\;{para}\;{obtener}{\mathrm{:}}}\\ & {}\\ & {\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}\mathrm{\cdot}\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}\mathrm{\cdot}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\sqrt{\frac{{\mathrm{(}}{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{))}}^{2}}{{1}\mathrm{{-}}{\cos}^{2}{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {{iv}{\mathrm{)}}\;{Utilizando}\;{sen}^{2}{x}\mathrm{{=}}{1}\mathrm{{-}}{\cos}^{2}{x}{\mathrm{,}}\;{se}\;{obtiene}{\mathrm{:}}}\\ & {}\\ & {\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{\sqrt{{\sin}^{2}\mathrm{(}u\mathrm{)}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{\sin\mathrm{(}u\mathrm{)}}}\\ & {}\\ & {\mathrm{\therefore}\;{La}\;{igualdad}\;{queda}\;{demostrada}{\mathrm{.}}} \end{align}$

[editar] Otras identidades trigonométricas

$\operatorname {sen} \left ( \frac{\pi}{2} - \alpha \right ) = \cos \alpha \,\!$

$\cos \left ( \frac{\pi}{2} - \alpha \right ) = \operatorname {sen}\alpha \,\!$

$\operatorname {sen} (\pi - \alpha) = \operatorname {sen}\alpha \,\!$

$\cos (\pi - \alpha) = - \cos \alpha \,\!$

$\operatorname {sen} (2\pi - \alpha) = - \operatorname {sen} \alpha \,\!$

$\cos (2\pi - \alpha) = \cos \alpha \,\!$

$\operatorname {sen}\alpha \cdot \cos \alpha + \operatorname {sen}\beta \cdot \cos \beta = \operatorname {sen}(\alpha + \beta) \cdot \cos(\alpha - \beta)$

$\begin{align} & {\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{)}}\mathrm{{=}}\arcsin{\mathrm{[}}\mathit{\alpha}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}\mathrm{{+}}\mathit{\beta}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}}\\ & {}\\ & {\mathrm{\vdash}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{)}}\mathrm{{=}}\arcsin{\mathrm{[}}\mathit{\alpha}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}\mathrm{{+}}\mathit{\beta}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}}\\ & {}\\ & {{i}{\mathrm{)}}\;{Usando}\;{cambio}\;{de}\;{variables}\;{tenemos}\;{que}{\mathrm{:}}}\\ & {}\\ & {{x}\mathrm{{=}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}}\\ & {}\\ & {{y}\mathrm{{=}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{)}}}\\ & {}\\ & {{ii}{\mathrm{.}}{i}{\mathrm{)}}{Se}\;{opera}\;{con}\;{el}\;\sin{\mathrm{(}}{x}\mathrm{{+}}{y}{\mathrm{),}}\;{entonces}{\mathrm{:}}}\\ & {}\\ & {\sin{\mathrm{(}}{x}\mathrm{{+}}{y}{\mathrm{)}}\mathrm{{=}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {{iii}{\mathrm{.}}{i}{\mathrm{)}}{Se}\;{obtiene}\;{el}\;{equivalente}\;{del}\;\cos{\mathrm{(}}{x}{\mathrm{):}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}{x}{\mathrm{)}}\mathrm{{+}}{\sin}^{2}{\mathrm{(}}{x}{\mathrm{)}}\mathrm{{=}}{1}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\sin}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{\cdot}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))]}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{(}}\mathit{\alpha}\mathrm{\cdot}\mathit{\alpha}{\mathrm{)}}}\\ & {}\\ & {\cos{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}}\\ & {}\\ & {{iii}{\mathrm{.}}{ii}{\mathrm{)}}\;{Se}\;{obtiene}\;{el}\;{equivalente}\;{de}\;\cos{\mathrm{(}}{y}{\mathrm{)}}\;{\mathrm{:}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}{\sin}^{2}{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{=}}{1}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\sin}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{\cdot}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))]}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{(}}\mathit{\beta}\mathrm{\cdot}\mathit{\beta}{\mathrm{)}}}\\ & {}\\ & {\cos{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}}\\ & {}\\ & {{ii}{\mathrm{.}}{ii}{\mathrm{)}}{Se}\;{sustituyen}\;{del}\;{paso}\;{iii}{\mathrm{)}}\;{el}\;\cos{\mathrm{(}}{x}{\mathrm{)}}\;{y}\;{el}\;\cos\;{\mathrm{(}}{y}{\mathrm{):}}}\\ & {}\\ & {\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{\mathrm{\{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))]}}\mathrm{\cdot}{\mathrm{(}}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}{\mathrm{)\}}}\mathrm{{+}}{\mathrm{\{(}}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}{\mathrm{)}}\mathrm{\cdot}{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))]\}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}{\mathrm{[}}\mathit{\alpha}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}{\mathrm{]}}\mathrm{{+}}{\mathrm{[}}\mathit{\beta}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}{\mathrm{]}}}\\ & {}\\ & {{iv}{\mathrm{)}}{Se}\;{obtiene}\;{el}\;\arcsin{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))],}}\;{para}\;{te}{\mathrm{rmin}}{ar}\;{la}\;{demostracion}{\mathrm{:}}}\\ & {}\\ & {\arcsin{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))]}}\mathrm{{=}}\;\arcsin{\mathrm{[}}\mathit{\alpha}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}\mathrm{{+}}\mathit{\beta}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}{\mathrm{]}}}\\ & {}\\ & {\mathrm{\therefore}\;{queda}\;{demostrada}\;{la}\;{igualdad}{\mathrm{.}}} \end{align}$

Véase también: Sinusoide

[editar] Seno y coseno, funciones complejas

El seno y coseno se definen en matemática compleja, gracias a la fórmula de Euler como:

$\operatorname {sen} \alpha= \frac {e^{i\alpha}-e^{-i\alpha}}{2i}$

$\cos \alpha= \frac {e^{i\alpha}+e^{-i\alpha}}{2}$

Por lo tanto, la tangente quedará definida como:

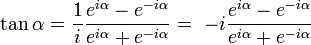
$\tan \alpha =\frac{1}{i} \frac {e^{i\alpha}-e^{-i\alpha}}{e^{i\alpha}+e^{-i\alpha}} =\ {-i} \frac {e^{i\alpha}-e^{-i\alpha}}{e^{i\alpha}+e^{-i\alpha}}$

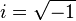Siendo $i=\sqrt{-1}$ (también puede representarse como j).
Es preciso destacar, que todas las formulas trigonometricas anteriores, son derivadas del Teorema de Pitágoras.